Appello online di Matematica Ragionata
In questa pagina ci sono 20 domande a risposta multipla, come quelle proposte nei test di ingresso alle università scientifiche. Ciascuna domanda è corredata dalla risposta e da una o più soluzioni al quesito.
Le soluzioni provengono dal libro Matematica Ragionata di Marita Dante: il libro contiene piu’ di 250 quesiti risolti. Visita il sito del libro per acquistare il volume o scaricare l’archivio degli appelli di Ingegneria.
Istruzioni e punteggio
- per ogni domanda una ed una sola delle risposte è corretta;
- le risposte esatte valgono 1 punto;
- le risposte errate valgono –1/3 punti;
- le risposte mancanti valgono 0 punti.
Quesito 1 – Algebra. L’equazione $|1-x^{2}|=2$
- ha esattamente una soluzione reale
- non ha soluzioni reali
- ha esattamente due soluzioni reali
- ha più di due soluzioni reali

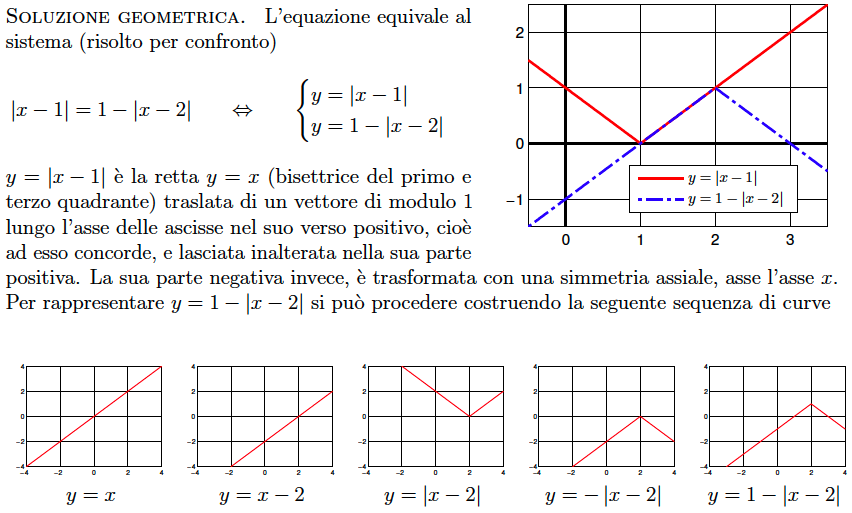
Quesito 2 – Algebra. Le soluzioni reali dell’equazione $|x-1|+|x-2|=1$
- sono $x=1$ e $x=2$
- non esistono
- sono tutti gli $x$ tali che $1\leq x\leq 2$
- nessuna delle precedenti possibilità è corretta

Quesito 3 – Disequazioni. L’insieme delle soluzioni $x\in\mathbb{R}$ della disequazione $|x^2-x-2|\leq |x|$
- è una semiretta inferiormente illimitata
- è una semiretta inferiormente limitata
- è un intervallo limitato
- nessuna delle precedenti possibilità è corretta


Quesito 4 – Esponenziali e logaritmi. Sia $x$ un numero reale diverso da zero. L’espressione $\log(5x^{2})$ si può anche scrivere:
- $2 \log(5 x)$
- $2 \log(\sqrt{5} x)$
- $2 \log(\sqrt{5} |x|) $
- $\log(10x)$
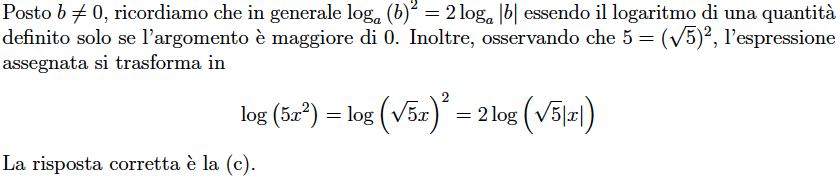
Quesito 5 – Esponenziali e logaritmi. Sia $x$ un numero reale. L’uguaglianza $\log((5-x)^{4})=4\log(5-x)$ è valida
- per ogni $x$
- per tutti gli $x < 5$
- per tutti gli $x$ tali che $-5 < x <5$
- per tutti gli $x > 0$

Quesito 6 – Esponenziali e logaritmi. Se $10^{(\log_{5}(\log_{7}x))}=1$ allora si ha:
- $x=5$
- $x=7$
- $x=10$
- nessuna delle precedenti possibilità è corretta

Quesito 7 – Esponenziali e logaritmi. Siano $x$ e $y$ numeri reali. Da $\log_{1/2}x<\log_{1/2}y$ si deduce
- $x>y>0$
- $0 < x < y$
- $|x|\leq|y|$
- nessuna delle precedenti possibilità è corretta

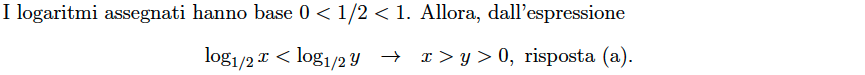
Quesito 8 – Esponenziali e logaritmi. La disequazione $\log_{10} \left( \log_{100} (x^{2}-1) \right) > 0$ è soddisfatta da tutti e soli gli $x$ tali che
- $|x|>\sqrt{101}$
- $|x|>1$
- $\log_{100}(x^{2}-1)>0$
- da nessun $x$

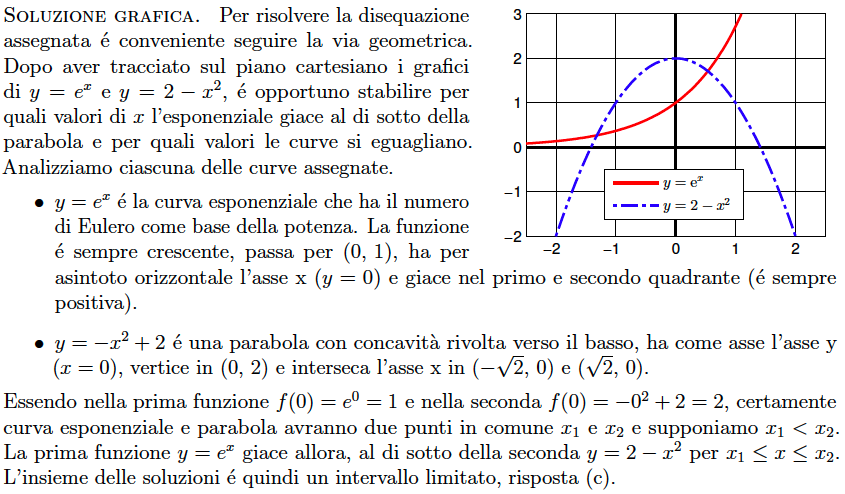
Quesito 9 – Esponenziali e logaritmi. L’insieme delle soluzioni $x\in\mathbb{R}$ della disequazione $e^x\leq 2 - x^2$
- è una semiretta inferiormente illimitata
- è una semiretta inferiormente limitata
- è un intervallo limitato
- è vuoto
Quesito 10 – Esponenziali e logaritmi. Il numero di soluzioni reali dell’equazione $\sqrt{x-1}=\log_{1/2}x$ è
- $0$
- $1$
- $2$
- superiore a $2$

Quesito 11 – Geometria Analitica. Le soluzioni del sistema di equazioni $x^{2}+3y^{2} =9$ e $|y| =x^{2}$ sono costituite da
- un punto del piano $(x,y)$
- due punti del piano $(x,y)$
- quattro punti del piano $(x,y)$
- non esistono punti del piano $(x,y)$ che risolvono il sistema

Quesito 12 – Goniometria e Trigonometria. Un angolo di un radiante espresso in gradi è circa uguale a (scartare eventuali cifre decimali)
- $57^\circ$
- $352^\circ$
- $87^\circ$
- $1^\circ$

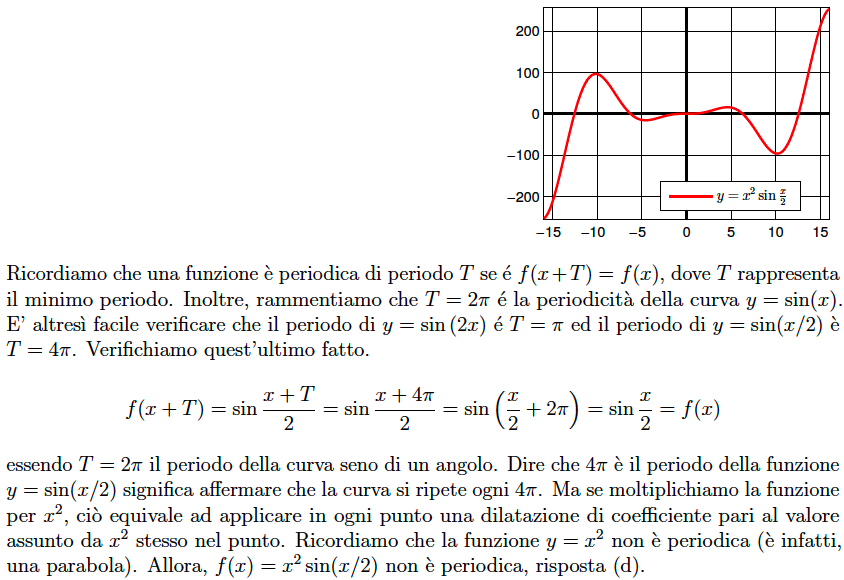
Quesito 13 – Goniometria e Trigonometria. La funzione $f(x) = x^{2} \sin(x/2)$ è
- periodica di periodo $ 4\pi$
- periodica di periodo $ 2\pi$
- periodica di periodo $4\pi\sqrt{\pi}$
- non è periodica
Quesito 14 – Goniometria e Trigonometria. Un triangolo ha due lati lunghi $4$ e $5$, e l’angolo compreso ha tangente $-\frac34$. Allora:
- il terzo lato è lungo $3$
- la lunghezza del terzo lato è minore di $3$
- il terzo lato ha lunghezza maggiore di $6$
- il terzo lato ha lunghezza compresa tra $4$ e $5$

Quesito 15 – Goniometria e Trigonometria. $\tan(\arccos\frac{5}{7})$ è uguale a
- $\frac{5\sqrt{3}}{6}$
- $\frac{\sqrt{6}}{5}$
- $\frac{2\sqrt{6}}{7}$
- $\frac{2\sqrt{6}}{5}$

Quesito 16 – Goniometria e Trigonometria. Sia $C$ la circonferenza di centro $(r,0)$ e raggio $r$, e sia $P$ un punto su di essa. Chiamiamo $\vartheta$ l’angolo formato dal semiasse delle ascisse positive con la semiretta uscente dall’origine e passante per $P$. Allora la distanza del punto $P$ dall’origine è
- $2r \cot \vartheta$
- $2r \cos \vartheta$
- $2r \tan \vartheta$
- $2r \sin \vartheta$

Quesito 17 – Goniometria e Trigonometria. L’espressione $\arccos (-2/3) \arcsin (2/3)$
- è $<0$
- non esiste
- è $>0$
- nessuna delle precedenti possibilità è corretta

Quesito 18 – Logica e Insiemi. L’esatta negazione della proposizione “Tutti i matematici sono strani” è
- nessun matematico è strano
- esiste un matematico strano
- esiste un matematico che non è strano
- nessuna delle precedenti possibilità è corretta

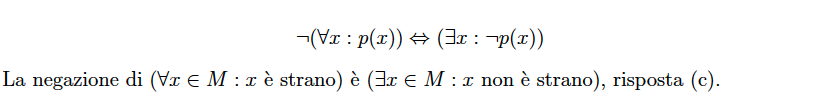
Quesito 19 – Logica e Insiemi. Supponiamo che sia vero che tutti gli studenti del corso $x$ che hanno studiato e hanno frequentato le lezioni hanno superato l’esame. Quale delle seguenti affermazioni è necessariamente vera:
- tutti gli studenti hanno superato l’esame
- se uno studente non ha frequentato le lezioni non ha superato l’esame
- se uno studente non ha studiato non ha superato l’esame
- se uno studente non ha superato l’esame allora non ha frequentato il corso oppure non ha studiato


Quesito 20 – Logica e Insiemi. Quale tra le seguenti affermazioni, riferite ad un triangolo, è falsa:
- essere equilatero è condizione sufficiente per essere isoscele
- non essere isoscele è condizione sufficiente per non essere equilatero
- essere isoscele è condizione necessaria per essere equilatero
- essere equilatero è condizione necessaria per essere isoscele


I quesiti e le soluzioni di questa pagina sono estratte provengono dal libro Matematica Ragionata di Marita Dante: il libro contiene piu’ di 250 quesiti risolti. Visita il sito del libro per acquistare il volume o scaricare l’archivio degli appelli di Ingegneria.
Copyright 2019—2021 Marita Dante. Tutti i diritti riservati.
Web design credits: Tim O’Brien